本工作表明,热膨胀实验可用于测量四种Ni基单晶高温合金(SX)的c固溶温度,其中一种具有Re和三种Re-free变体。对于CMSX-4,实验结果与使用ThermoCalc获得的数值热力学结果非常吻合。为了三种实验性的Re-free合金的实验结果和计算结果相近。透射电子显微镜显示,可以合理地预测c相的化学成分。我们还使用共振超声光谱(RUS)来显示弹性系数如何取决于化学成分和温度。根据文献中先前报告的结果对结果进行讨论。突出了需要进一步工作的领域。
图形概要
介绍
镍基单晶高温合金(SXs)用于制造可在高于1000 C的温度下运行的涡轮机叶片。它们必须承受载荷谱,包括蠕变,热疲劳和热腐蚀。蠕变强度是抵抗缓慢而连续的应变积累的抵抗力,这一点至关重要。众所周知,SX的强度依赖于微观结构,微观结构由亚微米长方体c颗粒和(晶体结构:有序L12相;体积分数:70 vol。%)组成,它们之间通过细小的c通道分隔开(晶体结构:fcc;体积分数:接近30%(体积)),例如[1-4]。两相的晶体结构相似,因此,从高温冷却后,有序的c粒子会凝聚并沉淀在c矩阵中。两相的晶格常数d不同。镍基单晶超级合金,经常发现:dc&\ dc。相关的晶格失配导致弹性应变能增加,例如[5、6]。这种错配及其一些后果,例如,它对c粒子形状的影响,以及对作用于通道位错,漂流和形成界面位错网络的桃子-科勒力的影响,现在仍在继续在文献中讨论过,例如[7-15]。有序的c &&粒子表示位错运动的障碍。
它们不是完全不可穿透的,但是位错通过有序的c相移动要比通过fcc和c通道移动更困难。SX设计的技巧部分取决于使位错切入c相以使其蠕变强度最佳化的难度尽可能大。 使切割变得困难与反相边界能量(APB)的增加有关,例如[16–20],这是由晶体可塑性中最突出的基本机理之一引起的:c相的成对切割,例如&[21] –23]。虽然就切削过程的具体方面在文献上存在分歧,但来自学术界和工业界的SX研究人员认为,设计具有高c体积分数,高&c固溶温度的合金是可取的。性能和化学成分,会产生较高的平面故障能量,从而影响APB和堆叠故障的物理性质。 c-&固溶温度被认为特别重要,在许多科学和技术SX出版物中,固溶温度已被作为参考温度加以强调,例如[24-31]。
本工作仔细研究了四种SX,ERBO / 1(含Re,一种CMSX-4型合金)和三种ERBO / 15变体(不含Re,Mo,Ti和W含量较高)的热力学性质。 。它使用共振超声光谱(RUS)和膨胀计来测量弹性刚度和热膨胀系数随温度的变化。最近已显示出这四种合金在蠕变性能方面有何不同[32、33]。
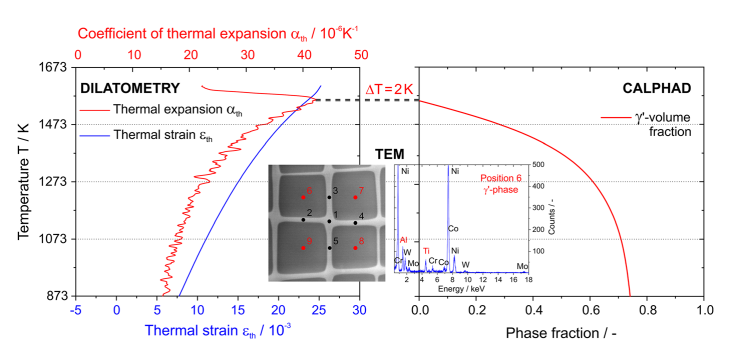
本工作研究了合金成分中的大(ERBO / 1与ERBO / 15对比)和小(三种ERBO / 15变形)变化如何影响其热弹性性能。第一个目标:比较两种不同的合金(合金成分差异很大)有助于朝着超级合金单晶技术的整体努力方向发展,在该技术中,昂贵且具有战略意义的合金元素(例如Re)已知具有很高的蠕变强度,在不影响机械强度的前提下被其他元素替代。在这方面,弹性和蠕变特性均很重要。已经提出,可以通过增加Mo,Ti和W的含量来实现这一点[34]。另外,在高温工程中需要弹性系数来设计部件,该部件需要承受热疲劳载荷。因此,在本工作中努力测量弹性系数。第二个目标:只有研究一种特定元素的作用后,才能获得对各个合金元素作用的详细了解。在这方面,三种ERBO / 15变体的比较很有帮助。第三个目标:特别是,探索和探索了高分辨率膨胀计作为确定高c-固溶线温度的方法的潜力。为此,我们将高温和高温膨胀法测得的c固溶温度的实验结果与理论ThermoCalc计算进行了比较[35]。通过比较其对使用3D原子探针X射线照相法(3D-ATP)[36]和透射电子显微镜(TEM)获得的Cand c相化学组成的预测,可以评估ThermoCalc预测的质量。建立高分辨率的热膨胀测量值作为确定c-固溶度的方法代表了超合金技术的重要进步。
根据先前发表在文献中的工作对结果进行了讨论。突出了需要进一步研究的领域。
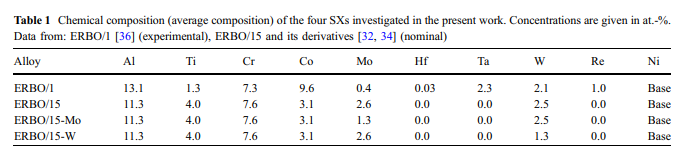
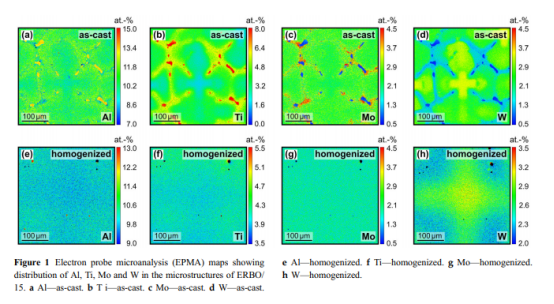
材料,实验和方法材料:在本工作中,研究了四种材料。表1列出了它们的标称化学成分。ERBO / 1是CMSX-4型合金,有关加工,多步热处理和微结构的详细信息已在其他地方发表[32,33,36,37]。 ERBO / 15是由Rettig等人开发的低密度Refree单晶镍基高温合金。 [34]使用数值热力学多准则优化方法。在当前的工作中,我们将ERBO / 15与两个更瘦的ERBO / 15变体进行比较,它们包含更少的W和更少的Mo(ERBO / 15-W和ERBO / 15-Mo)。表2列出了四种被研究合金的热处理细节。ERBO / 1在波鸿的Doncasters Precision Castings进行了热处理,而ERBO / 15变体的热处理则在定制的真空热处理炉中进行。来自Carbolite Gero,类型为LHTM 100–200 / 16 1G。有关热处理程序的详细信息记录在[32]和[36]中。使用用于ERBO / 1的电子探针微分析仪SX 50和用于ERBO / 15的SXFiveFE类型的场发射电子微探针及其两种衍生物(均来自Cameca)进行电子探针微分析(EPMA)。众所周知,在凝固过程中,SXs的合金元素在分配到树枝状和树枝状区域方面的趋势可能会有所不同。图1给出了铸态条件下(上排,图1a-d)和均质化热处理后(下排,图1)在ERBO / 15的微观结构中元素Al,Ti,Mo和W的分布。 1e–h)。图1的下一行显示,在均质化步骤中,可以降低与合金元素在凝固过程中的分配趋势相关的大规模化学异质性(表2);但是,它并没有完全消失,如图1h中的W所示。使用购自Carl Zeiss AG的Leo Gemini 1530 SEM进行扫描电子显微镜(SEM)研究,该设备配备了以12 kV操作的场发射枪(FEG)和透镜检测器(工作距离:4.5mm,孔径:30 mm)。
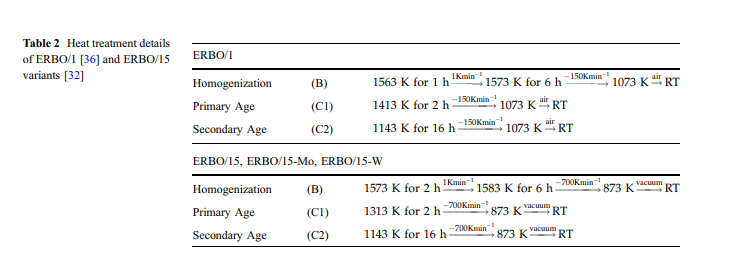
图2给出了八种材料状态的SEM显微照片,这些材料在本工作中已得到考虑。图2的上排显示了四个铸态材料状态。图2的下排显示了二次时效处理(表2)之后经过完全热处理的材料状态。
透射电子显微镜(TEM)用于分析c / c微观结构中两相的局部合金化学。使用&JEOL JSM-6490(用于ERBO / 1)和来自FEI的Tecnai G2 F20(用于ERBO / 15及其衍生产品)进行TEM,这两种设备均配备了在200 kV下运行的FEG和EDAX分析系统。该程序用于测量三种ERBO / 15变体的相组成,如图3所示。图3中间的图片显示了沿\ 100方向拍摄的STEM显微照片(多束对比度)。 。 EDX光谱是在五个c通道位置(如所示,为1-5)和四个相邻c粒子的中心(位置为6-9)获取的。在60 s的时间内以电子束直径\ 10 nm记录每个EDX和光谱。使用EDAX算法计算组成。获得这两个阶段的值,作为五个通道测量值(分析点1至5)和四个颗粒测量值(分析点6至9)的平均值。交叉c通道(橙色,位置1)和右上方c粒子(绿色,位置7)的EDX光谱示例分别在左右图中显示。
为了进行比较,我们使用了Parsa等人报道的一些局部组成结果。 [36],这是通过局部电极原子探针(LEAPTM 3000X HR,Cameca Instruments)在电压模式下以* 65 K的样品基础温度获得的。
共振超声光谱法(RUS):在当前工作中,借助于共振超声光谱法(RUS)确定弹性刚度系数作为温度的函数,例如。 [38,39]。通过将Laue取向与电火花腐蚀加工相结合,可以精确地获得100个目标尺寸约为8 9 7 x 6 mm3- = 336 mm3的定向立方体样品,如[40]中所述。在目前的工作中,对ERBO / 15及其变型进行了RUS测量。为了进行比较,ERBO / 1的数据取自Demtro¨der等人的工作。 [41]。所有样品的尺寸均在表3中给出。对于本工作中测试的所有样品,几何密度qG(根据样品重量和体积计算)与通过浮力法qB确定的密度(表3)之间具有良好的一致性。通过研磨和金刚石板抛光建立了良好的表面质量。

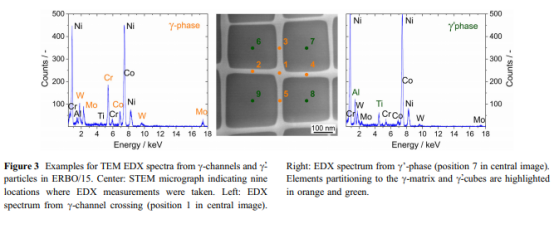
在图4a中,显示了一个典型的RUS样品夹在两个陶瓷棒之间,图3的示例是ERBO / 15中c通道和c-&粒子的TEM EDX光谱。中心:STEM显微照片,指示进行EDX测量的9个位置。左:c通道交叉处的EDX光谱(测量热电偶附近的位置1。在实验过程中,热电偶未附着到样品上,但非常接近。样品和热电偶的相关部分位于炉子的温度恒定区中。
为了实验确定共振频率,采用了自由振动的样品。实验获得的共振频率与假立方晶体[38、39、41]的三个独立的弹性刚度系数c11,c12和c44有关。为了收集数据,使用了内部构建的RUS设备。该系统由频率响应分析仪(NF Corporation的FRA5087型)和高速放大器(NF Corporation的BA4825型)组成,用于信号生成和检测。实验是使用Netzsch低温炉和级联温度控制器(Eurotherm的2704型)在100至673 K的温度范围内进行的。样品的共振光谱记录在150至1000 kHz的范围内。对于ERBO / 1,Demtro¨der等人。 [41]研究了室温到1273 K之间在50 K步长下的弹性特性。本工作的ERBO / 15变体以100 K至673 K在10 K步长下进行了研究。

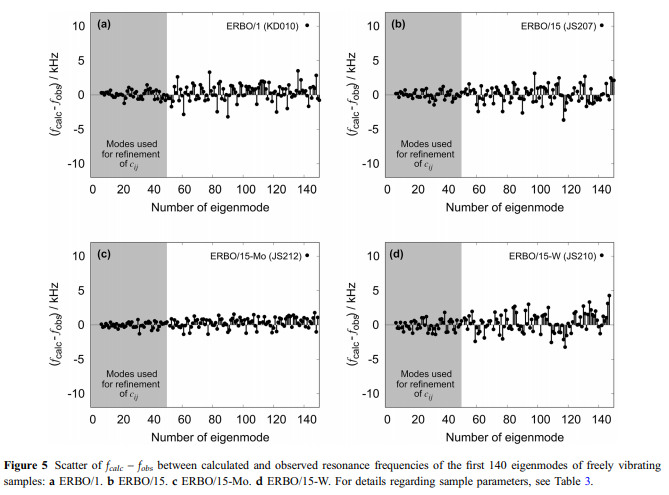
根据Demtroder等。 [41],与铸造微观结构(枝晶和枝晶间区域)相关的大规模异质性可能会影响与枝晶间距数量级的波长的共振。按照Demtro¨der等人描述的步骤。 [41],通过非线性最小二乘拟合程序,在具有最低频率的50个本征模(图5a-d中以灰色突出显示)的基础上,细化了所有样本的弹性系数。仔细观察在室温下实验观察到的共振频率fobs与根据精制样本参数fcalc计算的共振频率之间的差异,平均得出0.33到0.6 kHz的偏差,这证明了精制的良好质量。在图5中,根据从最低共振频率到最高共振频率的本征模式绘制了这些差异。 Demtro¨der等。 [41]表明,这种差异随着样本量的减少而增加。最重要的是,当样品尺寸超过树枝状晶体之间的平均间距至少10倍时,可以获得良好的结果。作者还得出结论,平均偏差小于2 kHz是可以接受的。从图5中可以看出,本工作中观察到的平均散射不超过该值。
膨胀计(DIL):高精度膨胀计用于监测热膨胀系数ath的温度依赖性。如[41]中所述,使用Netzsch公司的DIL402c型感应膨胀计,测量了热应变eth,即样品长度DL / L0(L0:293 K处样品长度)随温度的相对变化。 ]。如图4b所示(样品夹在两个陶瓷棒之间,热电偶闭合但尚未连接),用于测量热膨胀的样品具有与用于评估弹性的样品相同的几何形状和晶体学取向刚度,请参见表3。膨胀计已用刚玉制成的相同长度的标准样品进行了校准。所有实验均在He大气中以2 K / min的加热速率进行。线性热膨胀系数ath 1/4 oeth = oT被确定为相应应变温度曲线的一阶导数。为此,通过二阶多项式近似计算每个温度Ti周围±1.5 K间隔内的40个(应变,温度)数据对,由该二阶多项式计算athðTiÞ。
热力学计算:在多组分合金中,相稳定性取决于合金的化学性质,温度和压力[43-45]。如今,由考夫曼和伯恩斯坦[45]最初开发的CALPHAD方法(CALPHAD-PHAse图的计算的缩写)可以用于计算多组分合金中的相平衡[46,47]。在当前工作中,ThermoCalc(最新的CALPHAD实现)与数据库TCNi8,版本2019b [35]结合使用,用于计算热力学平衡,重点是c-和固溶温度以及c相和c相。此外,计算了所有四种合金的液相线和固相线温度以及c体积分数,并将其作为温度的函数。这些计算是基于我们的SX中合金元素的均匀化学分布。实际上,存在具有包含不同化学组成的树枝状(D)和树枝状(ID)区域的树枝状凝固。但是,如[36]所示,D和ID区域之间平均化学成分的差异是通过调整体积分数来解决的,两个区域中的c通道和c立方具有相同的成分。因此,就两相的化学组成而言,没有做出任何区分D和ID区域的努力。
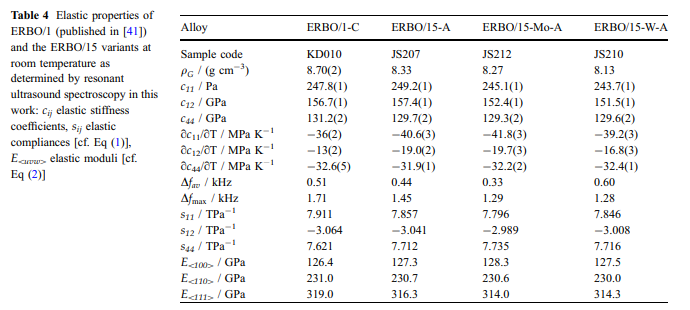
结果弹性性能:假单晶ERBO / 15及其变体在室温下通过RUS方法获得的弹性刚度列于表4。为进行比较,添加了来自文献[41]的ERBO / 1数据。此外,已经使用该关系计算了弹性柔量sij,该关系适用于具有立方对称性的材料。
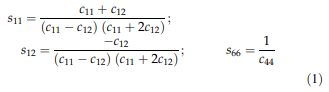
方向的杨氏模量或弹性模量E等于弹性柔度的纵向效应的倒数。在感兴趣的方向上,u = u1e1? u2e2? u3e3,其中ei描述笛卡尔参考系统的基向量,而ui是方向余弦,通过以下方式获得选定立方方向的E模量:
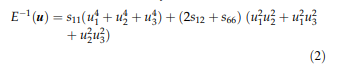
表4列出了选定的值。
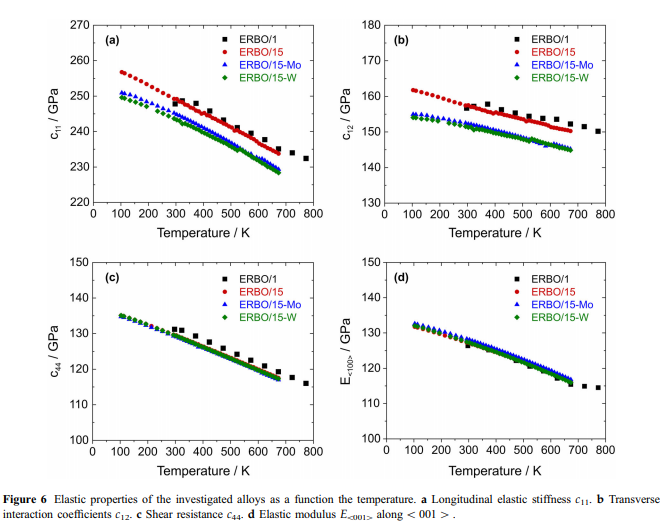
弹性刚度的温度依赖性如图6所示。在100和673 K之间,c11,c12和c44随着温度的升高而分别连续降低约8.5%,6%和13%。表4中给出了cij的温度系数,该系数是通过对273-673 K温度范围内的实验数据进行线性近似确定的。为了描述E模量在晶体学方向\ 100 [,\ 110 [和\ 111 [,相应的E \ uvw [数据是通过以下类型的二阶多项式在整个研究的温度范围内近似得出的:
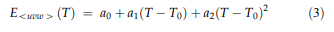
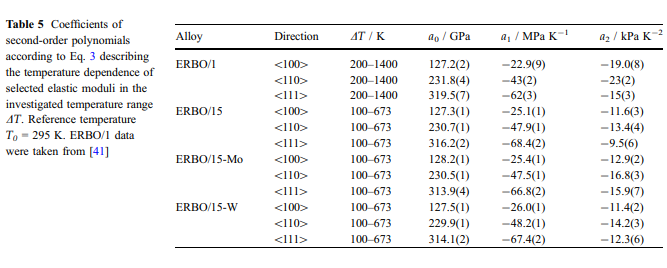
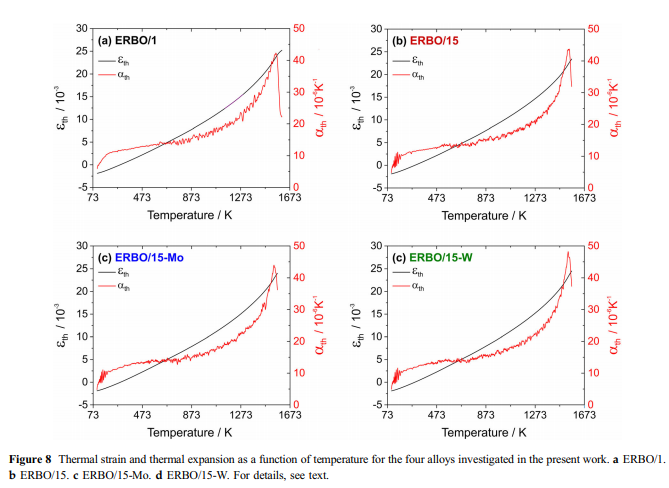
表5给出了从完全收敛拟合的协方差矩阵得出的相应参数及其标准偏差。例如,ERBO / 1的E \ 100 [值(来自[41]的数据)和ERBO / 15的值变体(这项工作)显示在图6d中。膨胀测量结果:四种被研究的高温合金的热膨胀结果在图2和3中给出。参见图7和8。实验应变曲线eth- = f(T)的特征都是在高温下可以很好地再现斜率的变化。当绘制热膨胀系数ath = f(T)作为温度的函数时,这一点尤其明显。这些曲线在高温下表现出急剧的热膨胀系数最大值。在图7中,显示了铸态和完全热处理的ERBO / 15-W的热应变和热膨胀系数。
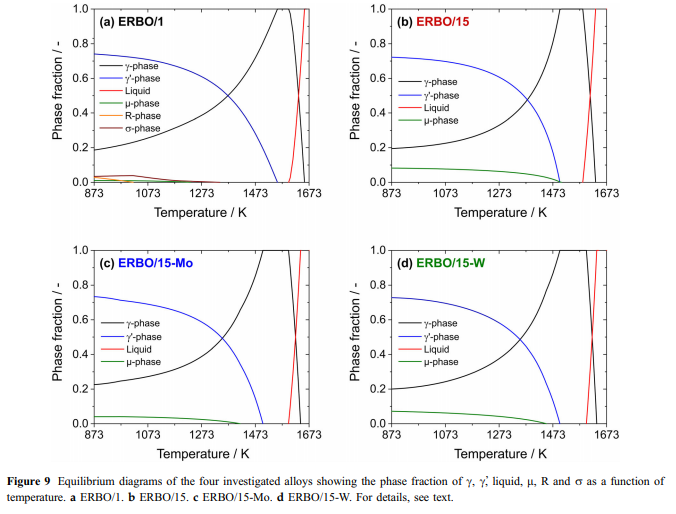
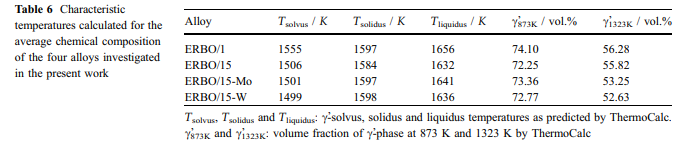
显示了ERBO / 15-W。可以看出,铸态和热处理材料的ath(T)峰值位置接近,热处理材料的峰值温度仅比铸态材料的峰值温度高12K。在热处理的材料状态下研究了ERBO / 1。对于ERBO / 15变型,分析了铸态材料的状态。 ThermoCalc预测和合金成分:根据表1中给出的化学合金成分,使用ThermoCalc计算所有研究合金的平衡相分数。图9中显示了这些成分与温度的关系。而在ERBO / 1中,这三个都是热力学的。平衡时会形成稳定的TCP相(l相,r相和R相),而ERBO15及其衍生物中只有l相形成。随着温度的升高,TCP和c相的馏分减少,而c相的分数增加。在表6中,列出了计算的固溶线(Tsolvus),固相线(Tsolidus),液相线(Tliquidus)温度,以及从图9所示曲线中获得的873 K和1323 K处的c相和馏分。显而易见的是,特别是针对ERBO / 1的计算的c固溶温度和比ERBO / 15及其衍生物的固溶温度高约50K。尽管计算得出的固相线温度非常相似,但ERBO / 1的液相线温度是所有四种合金中最高的。同样,在ERBO / 1的情况下,在873 K(74%(体积))和1323K(56%(体积))下计算出的c相分数&fV c&最高。当ERBO / 15中的Mo或W含量降低(通过增加Ni来平衡)时,计算出的固相线和液相线温度降低。降低导致在873 K(& 1 vol。%)时较高的c相分数,但在1323 K(&-3 vol。%)时c分数较低。
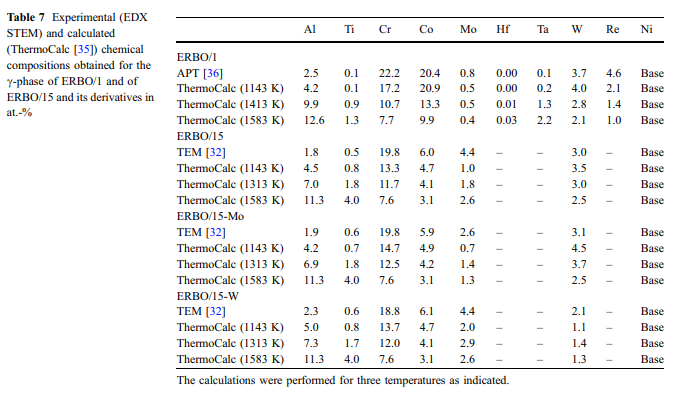
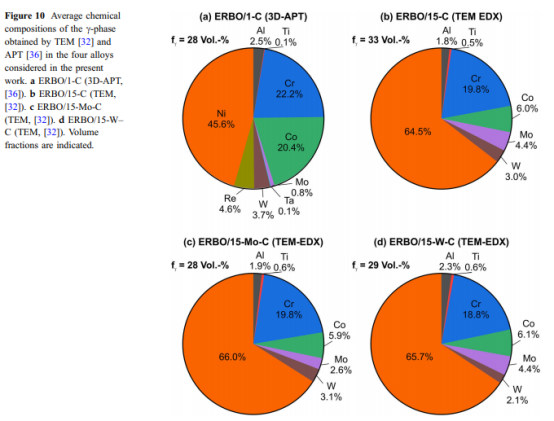
计算和测量的相组成:使用3D APT(ERBO 1)[36]和TEM-EDX(ERBO 15及其衍生物)测量了四种研究合金中的c相和c相(&cc和cc&)的组成。 [32]。这两个阶段的实验结果列在表7(c相)和8(c-&相)中。表7和表8还包含在1133 K(所有合金的第二个沉淀处理步骤的温度),1413 K和1583 K(ERBO / 1;分别是第一沉淀处理步骤和均质化的温度)和温度下获得的ThermoCalc预测值。 1313 K和1583 K(ERBO / 15变型;分别为第一沉淀处理步骤的温度和均质化)。由于c相的体积分数小于c相,因此其化学成分的变化更加明显。在无花果中。参照图10和11,我们以饼图的形式给出了表7中c相的化学组成。图10显示了实验数据,这些数据是在蠕变之前在所有四种热处理合金中测得的。图11显示了ERBO / 1(1143、1413和1583 K)和ERBO / 15(1143、1313和1583 K)c相的ThermoCalc预测。
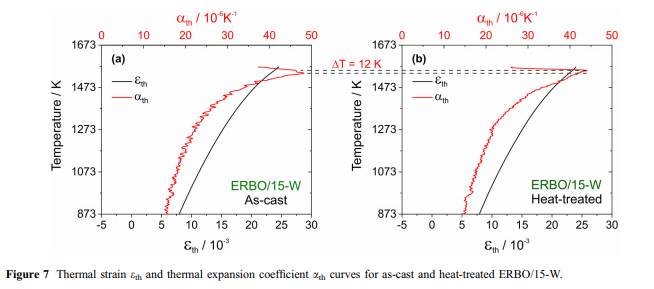
表7和图5和图6中呈现的数据是表1中的数据。图10和11(c相)和表8(c相,显示的数据且没有图形)显示,温度升高导致Ti,Al和Ta含量增加,同时Cr,Co,W和Re含量降低ERBO / 1处于c相。从图11所示的ThermoCalc结果中可以看出,基本元素Ni的含量随ERBO / 1中温度的升高而增加。相反,它在ERBO / 15中随温度升高而降低。分别在&表7(以及图10和11)和表8中的c相和c相的热力学数据进一步表明,对于两种合金系统,1143 K(实验合金的最后沉淀处理温度)和实验确定的数据并不完全一致,而是彼此相当接近。仅在ERBO / 15的情况下,元素Mo在1143 K(1.0 at。%)的计算中显示的值显着低于实验(4.4 at。%)。
讨论弹性刚度:如图6a–c所示,所有弹性刚度均随温度升高而降低。这主要是晶格电势不和谐的结果。随着温度的升高,增加的热振动会导致更大的键合距离,从而导致键合相互作用降低,从而导致弹性刚度降低。 ERBO / 1和ERBO / 15的弹性行为几乎相同,而c11和c12的更瘦的ERBO / 15变体的结果则略短。这不会显着影响所有的弹性模量E \ 100 [(图6d)。如表9所示,SX的各个合金元素的尺寸,晶体结构,杨氏模量,电负性和熔点不同[48-51]。图6d表明,本工作中考虑的合金化学变化不会强烈影响弹性性能。这与Demtro¨der等人得出的结论是一致的。 [41],他的研究表明,合金成分的变化比当前工作中所考虑的更大,不会强烈影响SX的弹性。单晶的弹性行为直接反映了其键合系统的各向异性。后者主要由晶体结构中最近邻触点的类型,数量和空间排列控制。由于Ni基SX的结构(包括c / c'-微结构)及其主要化学成分([62 at-%Ni,[11 at-%Al])仅略有不同,因此相互作用主要由Ni–Ni和Ni–Al接触,仅导致宏观弹性刚度的很小变化[42]。
热膨胀和c固溶温度&:热膨胀与材料随温度升高而改变其体积的趋势有关。在晶体中,这与原子振动能的增加和晶格势的非谐波形状有关。根据格鲁尼森关系,aðTÞ与热容量成正比;反之,热容量与热容量成正比。因此,热应变eðTÞ可以用爱因斯坦模型的积分形式描述[52,53]:
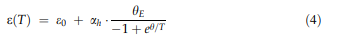
e0表示0 K时的初始应变,ah表示热膨胀系数的高温极限,hE表示爱因斯坦温度。关于温度的一阶导数得出热膨胀系数:
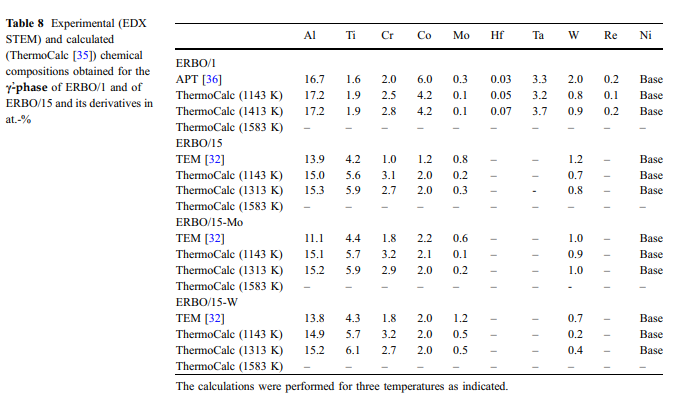
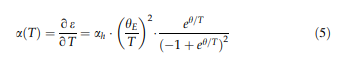
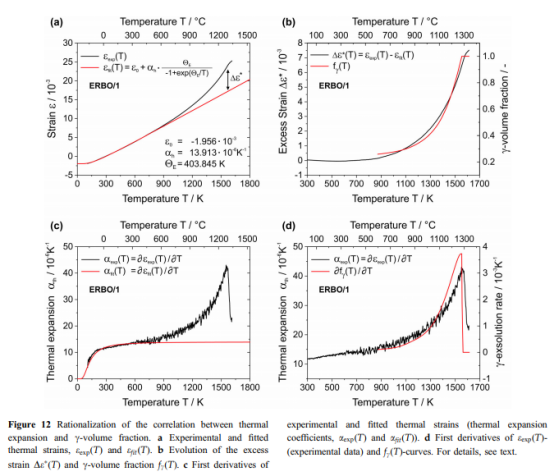
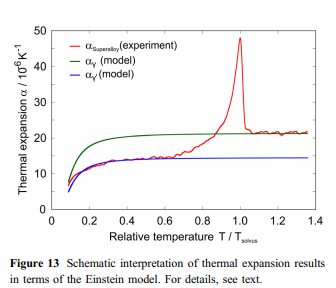
爱因斯坦模型通常可以在大约hE / 2以上的温度下提供良好的热容和热膨胀近似值。在这项工作中研究的高温合金的情况下,爱因斯坦方法很好地描述了观察到的热应变和热膨胀系数,最高可达800 K,hE在396和412 K之间变化(图12a,c)。然而,在较高的温度下,会出现如图12a所示的热过剩应变引起的显着差异,这代表了实验热应变eexp(T)(黑色曲线)和外推应变efit(T)(红色曲线,Eq)之间的差异。 3)通过将爱因斯坦模型拟合到800 K以下的eexp(T)来确定。实验曲线进一步经历了斜率的变化,考虑到图12c中的一阶导数aexp(T)黑色曲线,可以更好地理解该曲线。在图12b中,展示了De(T)(黑色曲线)以及ThermoCalc预测的c体积分数fc(T)(红色曲线)的演变。可以清楚地看到,两条曲线都显示出相似的趋势,这对于它们的一阶导数来说更加明显(图12d)。这有力地暗示了检测到脑曲线的斜率变化的温度,即,ath(T)曲线显示出尖峰的温度,代表了c-固溶温度。据报道,镍-铁-铝三元合金[54],CMSX-2 [55]和钴基合金[56、57]具有相似和相似的作用。图13示意性地示出了如何合理化实验观察到的热膨胀。在一阶近似中,可以假设两个孤立相的热膨胀分别遵循爱因斯坦模型(方程5)。不同的模型参数导致以下事实:在高温下,c相(绿色曲线)的值明显高于c相(蓝色和曲线)。红线示意性地示出了包含两个相的高温合金的实验数据(图3)。 T \ 800 K时,c相的热膨胀(高的初始c体积分数接近70%)占主导地位。从大约800 K开始,c沉淀逐渐析出,并逐渐析出。c相体积分数的相应增加(图12b)与调整两相的化学平衡组成有关。单位晶胞尺寸和c / c体积分数比率的最终变化导致尖峰和在实验测量的热膨胀中接近Tsolvus(图7、8、12c和d)。可以通过降低晶格失配的影响(图ERBO15及其变体的估计:5 9 10-3)来合理化图12a中所示的过量应变De *的50%,这为热应变提供了额外的贡献。 De *的其余部分可能与两个相的晶胞尺寸的变化有关,这与构型熵的增加有关。另外,c相的体积分数随温度的升高而增加,与c相相比,其热膨胀系数更高。这与来自文献的有关CMSX-4 [&58]分离的c和c相的热膨胀的实验数据以及在CMSX-4报道的大约870 K的热容量小阶梯式增加相一致。在[59]中。
随着温度的升高,空位密度增加,正如Simmons和Balluffi的开创性研究中报道的Al [60]。但是,这种影响通常很小,并且会随着材料的熔化温度呈指数增加。它与在实验ath(T)曲线中观察到的尖峰无关。例如在CuAu [61]和Ag3Mg [62]中的有序/无序转换中也报道了类似的效果。图8的膨胀测量结果与图9的CALPHAD预测结果在图14中进行了组合。膨胀曲线在高温下显示出急剧的热膨胀最大值,这对于ERBO / 1-C(1557 K)与ThermoCalc预测的c固溶度和温度(1555 K)(图14a)。但是,对于所有三个铸态ERBO / 15变体,在一定温度下观察到的ath(T)-最大值比ThermoCalc预测的c-固溶度和温度高约40 K(图14b-d)。在表10中,图1和图2中的峰值温度为0。显示了所有四种研究合金的7、8和14。
在图15中,我们将ERBO / 1热膨胀数据(以红色表示)与文献中公布的结果进行了比较。 到目前为止,我们已使用的弹性ERBO / 1数据表示真实的ath数据(红色实线),该数据如本实验部分所述获得。 在图15中,我们显示了这些数据以及平均值ath数据,这些数据是根据295 K作为参考温度根据以下公式计算的:
