轴裂纹转子动力学

产品介绍 

  航空燃气轮机和涡轮机振动诊断的重要方向是建 模诊断。建模提供了一个机会，将某些机器缺陷的存 在与振动信号中存在的迹象联系起来。其中一个缺陷 是航空发动机和涡轮机轴出现裂缝是不允许的。因 此，诊断系统重要的任务是及时检测裂纹并预测其 进展。转子中出现裂纹，导致局部刚度降低。刚度损失 的值取决于裂纹的几何特性。如果施加重力等静载 荷，转子旋转时裂纹打开和关闭。因此，轴的刚度每 一个周期都会发生变化。转子系统的裂纹导致振动信 号[1]发生以下变化： · 由于刚度降低引起的静态偏转的增加，转速1 倍谐波振幅增加。 · 由于转子刚度不对称，转速的2倍分量的外 观。 · 由于裂纹的周期性开闭而旋转的3х转速部件 的出现。该数学模型的主要任务是考虑尽可能多的因素， 描述裂纹发生部位刚度局部变化的值和规律。 有几种方法可以模拟裂缝。在较简单的情况下， 通过降低整个轴[2,3,4]的径向刚度来模拟裂纹。在其 他情况下，发生裂缝的轴部分被等效的梁元件所取 代。计算这些元素的刚度矩阵的系数，考虑裂缝和变 化的每个周期。在工作中，利用考虑裂纹的梁截面的 惯性矩计算有裂纹的梁构件的刚矩矩阵。在工作中， 根据固体破坏力学方程计算了该元素的[6]刚度矩阵。 可通过连接轴位置的边界部分来模拟裂纹，并给出裂 纹力矩刚度[7,8]。 当转子旋转时，根据其开关的不同而产生的裂纹 刚度的变化，可以用不同的数学方法来描述。在最简 单的情况下，可以假设裂纹只有两个位置：完全 打开或完全关闭，阶跃函数可以用数学方法来描述其 刚度变化[4]。Work[3]描述了最广泛的刚度变化模 型。其中之一是加斯奇方程。刚度的变化取决于静力 相位和裂纹相位之间的夹角，由傅里叶级数的17次谐 波描述。同一篇文章给出了梅斯和戴维斯方程，其中 刚度随角度根据余弦定律而变化。在杨模型中，刚度 随余弦定律的变化 研究人员提供的深度。 本文在现有方法的基础上建立了裂纹模型，并提 出了突出精确转子检测指标的方法。 该算法包含在动力学R4软件程序[9]中，该程序 代表了对复杂转子系统动态行为计算的专用系统。

裂缝模型 

  在公认的模拟概念中，轴模型中的裂纹被替换为 一个弹性链接，将轴分为两个部分，并用可变系数的 刚度矩阵来描述。如果无裂纹，则完成轴部件部分之 间的应变相容性条件，因此禁止所有相互位移。我们 介绍了位于裂纹区域的旋转坐标系ηOε，图1。它的 起源与固定坐标系XYZ的起源重合。轴执行两个运动， 绕Z轴适当旋转和进动。当描述裂纹时，我们只考虑围 绕η轴和ε轴的旋转。在其他自由度下的位移被忽略 了。

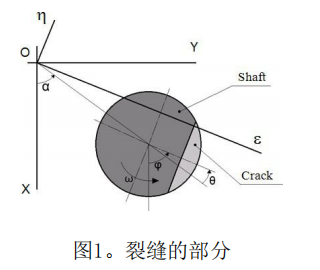
旋转坐标系中模拟裂纹的弹性矩阵可写如下：

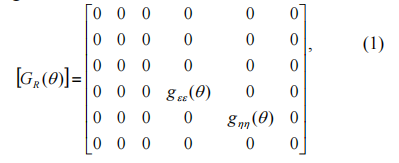
  在哪里q = j -a相位差，jj -轴的旋转不同角度，α - 进动角；  gee (q)和ghh (q ) - 变量弯矩弹性系数。

  灵活性取决于角度q因为当轴旋转时，裂纹会打开和关闭。 刚度矩阵是通过对 [GR (q)]矩阵求逆得到的，主对角线上的零柔度系数导致获得趋于无穷大的刚度系数。 我们将此类刚度系数的值限制为 1е10 N/m； 这个假设对结果没有显着影响，即我们得到

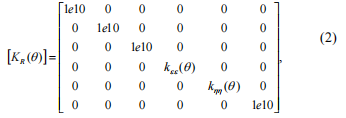
使用以下等式将刚度矩阵转换为固定坐标系：

在哪里[T]-旋转矩阵（4），在哪里C1 = cos(j), S1 = sin(j).

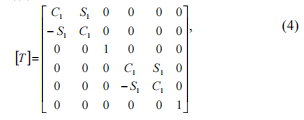
乘以与等式（3）对应的矩阵，我们得到：

    我们进行了一些转换，使我们有机会更简单地描述裂纹刚度矩阵及其系数获取算法。 与 Maes 模型相对应，可以假设有裂纹的圆梁的径向柔度由余弦定律从最小值变为最大值。

 其中 g0 - 无裂纹梁的柔度（最小值），gc - 有开裂梁的柔度（最大值）。

 我们用弯矩刚度k^init _mh   的铰链代替裂纹。 梁边界条件应提供其静态可定义性，如图 2 所示。

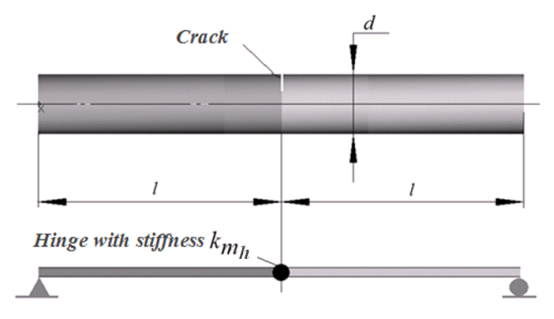
图2 铰链置换裂纹

则得到开裂轴突出部分的径向挠度为：

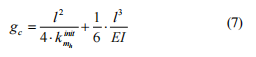
   其中 E - 杨氏模量，I - 轴截面的径向惯性矩，kinit mh - 对应于完全开放裂纹的等效连杆的力矩刚度系数。

    该方程有两个被加数——与裂纹有关的柔度和无裂纹梁的柔度。 它需要注意的是，无论梁的形状、边界条件和裂纹位置如何，其对一般梁柔韧性的贡献仅取决于系数 kinit mh ，即 第一个求和。

   当梁旋转时，裂纹截面的柔韧性会发生变化。 我们得到以下信息：

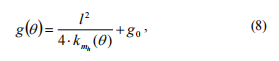
    哪里 g_o=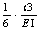-无裂纹梁的柔韧性，(q) k_mh- 给定q的当前力矩刚度系数。

将两个方程（5）和（7）积分，我们得到：

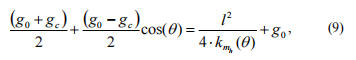
    其中服用式（6）考虑我们得到变化的规律力矩刚性取决于阶段 q 差异：

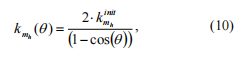
     获得的等效连杆的力矩刚度仅取决于轴直径、材料特性和裂纹深度。 轴中裂纹位置的变化，包括支撑单元在内的轴的特性不会改变等效连杆的力矩刚度（在

条件是有裂纹的截面在有裂纹的截面的任何部分保持不变

获得）。

   回到之前得到的刚度矩阵，其刚度系数可写为：

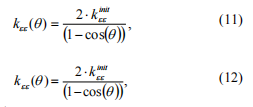
其中 k ^init_ee , k^init_hh  -全开裂纹对应轴上的力矩刚度初始值。

 k^init_ee  , k^init_hh 计算的任务可以通过两种方式解决。 第一个是矩的计算FEM 程序中的刚度。 二是运用断裂力学理论。 如果已知开裂的几何形状、轴直径和材料特性 [7,10]，则可以计算开裂局部挠度系数的值。

   带裂纹转子系统的仿真算法

   应通过以下步骤来获得裂纹的力矩刚度系数。

1. 完整的转子模型是在专门的程序之一中创建的，用于分析转子动力学（对于例如，在 Dynamics R4 中）。

2. 有裂纹的转子部分高亮显示。

3. 裂缝将轴段分成两个子系统。 由变量矩阵描述的链接

刚度系数 [K(q,j)]的尺寸为 6x6 放置在子系统之间。

4. 开裂的初始力矩刚度系数k^initee  , k^init_hh 由给出的方法得到多于。 这些数据是用于计算的初始数据。

结合运动方程计算连杆模拟裂纹刚度矩阵系数

每个q的转子系统。 在描述非线性动力模型的非线性陈述矩阵方程转子系统如下：

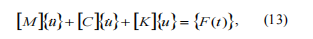
       其中[M ] – 惯性系数矩阵; [C] – 阻尼和陀螺仪系数矩阵 [K] - 刚度系数矩阵; { u&&} ,{ u&} ,{u} – 相应的振动加速度、振动速度和振动位移列; {F(t)} - 任何类型的动态载荷——内部和外部。

等效连杆的刚度矩阵可分为常量和变量两部分，下列为真：

   [KC ] 包含在 [K] 系统的一般刚度矩阵中。 矩阵 ( ) [ q j ] n , K 用于计算非线性连接的反应：

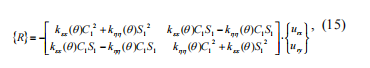     其中u_rx , u_ry– 截面围绕相应轴的相互旋转。系统的最终运动方程为：

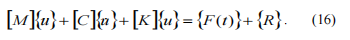
 给定的方程可以用数值方法求解，如 Runge-Kutta 法、Newmark 法等。

    建议算法的充分性是通过比较两个支撑梁的灵活性与

在有限元系统中并根据 Dynamics R4 中的假定算法获得的裂纹。 任务是计算裂纹和力之间不同阶段的裂纹截面中单位力作用下的梁挠度。

    图 3 显示了建议算法的检查结果。 比较三个结果：

- 使用有限元法 (FEM) 计算柔韧性。 在有限元系统中计算了裂纹梁模型的径向柔度，适用于裂纹角位置的整个范围；

- 使用 Dynamics R4 计算灵活性，使用 FEM 获得初始数据。 

    全开裂纹的力矩刚度初始值 k^init_ee , k^init_hh是求解方程（7）的k^init_mh得到的，并用有限元法计算相应方向有裂纹 gc 的梁的径向柔度。 根据（10）定律，中间角裂纹位置的弯矩刚度从较小值变为较大值；

   - 使用 Dynamics R4 计算灵活性。 完全开放裂纹的弯矩初始数据 k^init_ee  , k^init_hh  使用断裂力学算法[7, 10] 解析获得。 力矩灵活性值中间角裂纹位置根据定律 (10) 从较小值变为较大值。

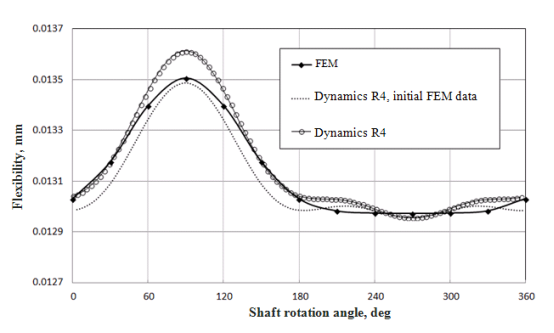
图 3 每转一圈裂纹截面梁柔度的变化

  FEM 模型的计算结果与 Dynamics R4 中的模型计算结果相近。 通过分析获得的初始条件的计算结果与 FEM 结果的差异小于 1%。 同时，初始刚度的分析计算速度比 FEM 计算快得多，并且需要更少的工作时间，因此更易于使用。

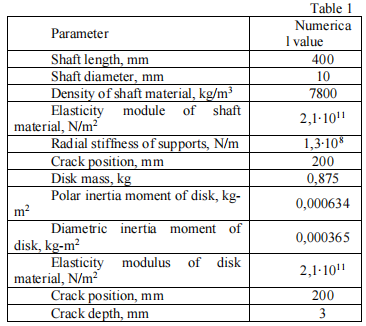
有裂纹转子的几何形状和参数

   选择带裂纹转子的几何形状以显示算法工作的最佳优势，如表 1。带有中心盘的转子，支架放置在轴端。

仿真结果

为了显示裂纹对动态转子行为的影响，转子加速度在 0 到

4000 转。 只有重力有外部影响。 这种转子的第一个临界速度为w_cr =2643,6 rpm (44,06 Hz)。 图 4 显示了获得的幅频特性。

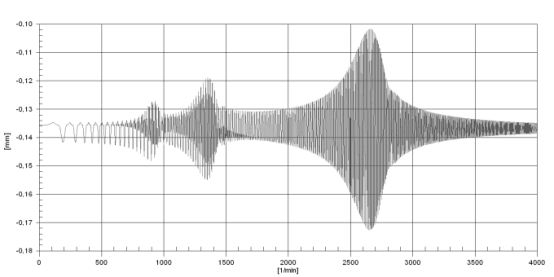
图 4 裂纹截面的幅频特性

    在距临界速度 1/3 和 1/2 处，参数共振是力矩循环变化的结果出现僵硬。 级联图显示了 1x、2x 和 3x 转子谐波，图 5。

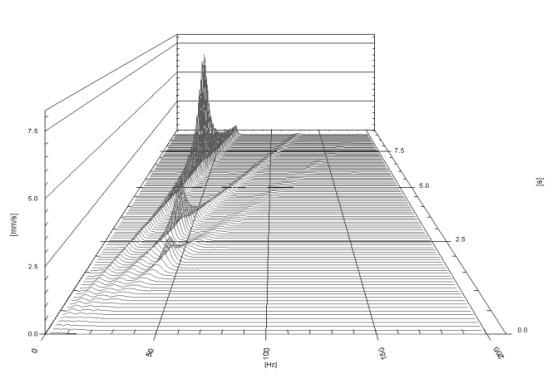
图 5 转子加速至 4000 rpm 时的振动速度级联图

下面给出了动态转子特性（光谱和轨道）在w =1/3w_cr , w =1/ 2wcr ,w = w_cr 。 只有转子重量代表外部载荷。

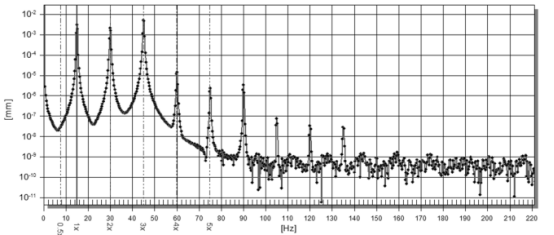
图 6 对数坐标中1/3 w_cr区域的信号频谱

图 7 线性坐标中1/3 w_cr 区域的信号谱

图 81/3 w_cr状态下裂纹截面转子中心轨道

图 9 对数坐标中1/2 w_cr区域的信号谱

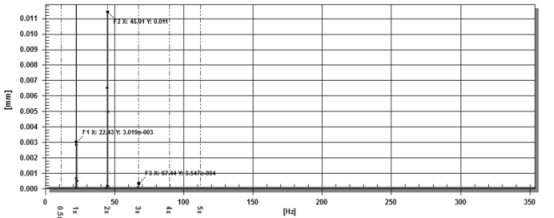
图 10 线性坐标中1/2 w_cr 区域的信号频谱

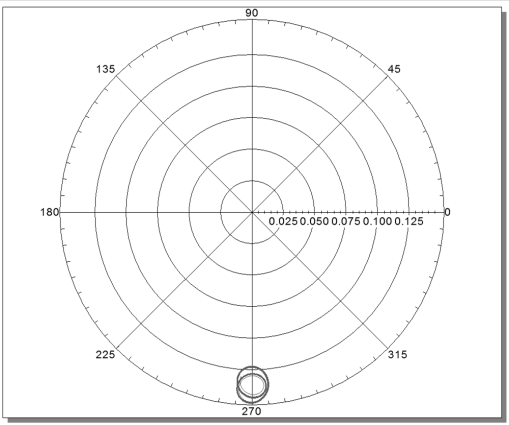
图 11 1/2 w_cr 状态下裂纹截面转子中心轨道

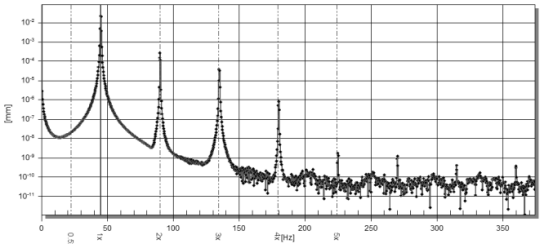
图 12w_cr 区域的对数坐标信号谱

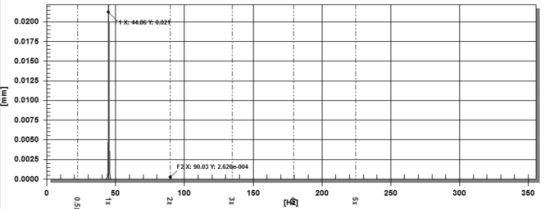
图 13 线性坐标中w_cr区域的信号谱

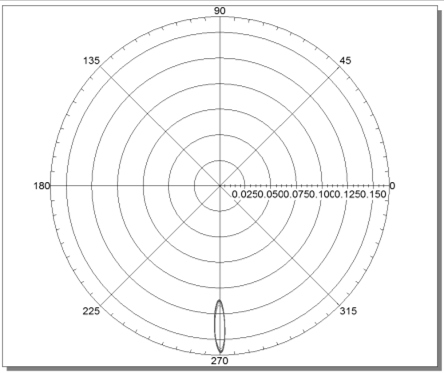图 14w_cr 状态下裂纹截面转子中心轨道

  获得的结果表明，次谐波共振的出现可能是裂纹出现的诊断标志。 检测多个转子谐波的最佳诊断机制是第一临界速度的 1/3 范围。 转子频率的三个谐波幅值接近于它。

    结论

    开发的裂纹模型在带裂纹转子动态特性分析算法中的应用

大大减少了建模和分析所需的时间。计算结果表明，轴的裂纹所研究的转子在1/3 w_cr , 1/3 w_cr , w_cr 状态下引起参数共振，这是转子的结果频率为 1x、2x、3x、4x 等的谐波。在实际测试中，有机会突出显示两个或三个转子谐波。存在次谐波共振、多次谐波和轴运动轨道的变化断面可能有裂纹出现的迹象。同时应该考虑到的概率在实际实践中检测裂纹取决于其几何形状和深度、所用设备的灵敏度、轨道传感器的存在等。因此，所提出的模型应主要被视为在振动诊断领域培训工程师的工具，并获得限制裂纹诊断标志的值。